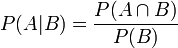[筆記] 17.NOV.11 Data Mining 上課筆記

今天的上課重點是

授課教授：交通大學 交通運輸研究所 陳穆臻 教授
參考書籍：Introduction to Data Mining, Tan, P. T., Steinbach, M., Kumar,. Vipin

１. PEBLS（Parallel Exemplar Based Learning System）
２. Bayes Classifier 貝氏分類
３. Naive Bayes Classifier 單純貝氏分類
４. 課後作業

１. PEBLS（Parallel Exemplar Based Learning System）


這是最鄰近法的改版，顧名思義，這也是已案例為學習方式的演算法，加入平行運算可以更快速的完成。
較為特別的地方是，他可以用來處理連續型資料（Continuous）與名義（Nominal）尺度的資料，其中名義尺度的資料採用MVDM（Modified value difference metric）方式處理，也就是修正後再比較的方式。

另外，每筆資料都會給相似度權重，因為是最鄰近法，所以預設K=1。

MVDM（Modified value difference metric）使用的公式如下：

其中，i為Class Level，如果Class為Yes與No的話就是 0、1，若為是、否與不一定，的話就是0、1、2，依此類推。n為目標屬性的資料數量。

MVDM（Modified value difference metric）舉例說明：

若我們想要算三個婚姻狀況Marital Status的分類之間的差異，我們的算法為分三個階段

1. d(Single,Married) ＝｜2/4－0/4｜＋｜2/4－4/4｜＝1
上述式子為，我們要計算未婚與已婚之間的差異，其中未婚共有4筆資料，已婚有2筆資料，分類為Yes的情況下差異為未婚4個之中有2個減去已婚4個之中有0個。分類為No的情況下差異為未婚4個之中有2減去已婚4個之中有4個。最後兩者相加的到差異為1

2. d(Single,Divorced) ＝｜2/4－1/2｜ + ｜2+4－1/2｜＝0
3. d(Married,Divorced)＝｜0/4－1/2｜＋｜4/4－1/2｜＝1

若我們要改計算償還屬性類別的差異，我們的算法如下：
d（Refund = Yes，Refund = No）＝｜0/3－3/7｜＋｜3/3－4/7｜＝6/7

最後，我們要計算記錄之間的差異的話，就要考慮到所謂權重的問題

採用的公式如下：

其中後半段公式為前面敘述的MVDM，算出距離與距離間的差異，接著在算兩個資料的權重。

其中，權重的算法為：

所以可以看得出來，當Wx越接近1表示X這筆資料預測的正確越高，表示每次用來預測都能夠正確預測成功。


２. Bayes Classifier 貝氏分類


貝氏分類是從貝氏定理演變來的，基本上與貝氏定理的意思是差不多了，所以先簡介一下貝氏定理。

假設Z為沒有生病機率51％，事件A為得了感冒機率25％，事件B為得了腸胃炎機率24％，事件C為感冒又腸胃炎機率5％。以下參考WIKI貝氏分配（http://zh.wikipedia.org/wiki/Bayes%E5%AE%9A%E7%90%86）
因此，在A事件發生的情況下，又發生B事件的機率為

＝ 5％ / 25％ ＝ 20％

而在B事件發生的情況下，又發生A事件的機率為

＝ 5％ / 24％ ＝ 20.8％

因此整合兩個式子，我們可以得到

Ｐ（Ａ｜Ｂ）．Ｐ（Ｂ）＝Ｐ（Ａ∩Ｂ）＝Ｐ（Ｂ｜Ａ）．Ｐ（Ａ）

20.8％ * 24％ ＝ 5％ ＝ 20％ * 25％

最後，在使用機率的乘法定理左右同除上Ｐ（Ｂ）得到

 也就是 20.8％＝（20％*25％）/ 24％

接下來進入正題，貝氏分類（Bayes Classifier）
設每個屬性為（A1,A2,A3,....An）
設屬性分類為C1,C2,....Cn，（假設你分類是Yes與No，那C就是C1與C2）
今天一筆未知的資料近來，我們要怎樣分類屬性呢？

方法如下：
1.假設我們目標分類是Yes與No，分別為Class1與Class2
2.假設我們屬性有三個，分別為A1、A2、A3
3.接著計算Ｐ（C1｜A1,A2,A3）與 Ｐ（C2｜A1,A2,A3）
根據貝氏定理我們可以得到

4.最後，挑選Ｐ（C1｜A1,A2,A3）與 Ｐ（C2｜A1,A2,A3）中最大的，作為我們的屬性分類。
雖然步驟是上面這樣，但我們要怎麼計算Ｐ（A1,A2,A3｜C）* Ｐ（C）呢？


３. Naive Bayes Classifier 單純貝氏分類

根據上節最後提到的要怎麼計算Ｐ（A1,A2,A3｜C）* Ｐ（C），這邊先介紹單純貝氏分類（Naive Bayes Classifier）的方法。
單純貝氏分類，有個重要的假設前題就是「屬性間是互相獨立的」，
因此我們可以將Ｐ（A1,A2,A3｜C）拆解成 Ｐ（A1｜C）、 Ｐ（A2｜C）、 Ｐ（A3｜C）

因為我們的C有Class1與Class2，所以要計算共六次，分別為
Class1：Ｐ（A1｜C1）、 Ｐ（A2｜C1）、 Ｐ（A3｜C1）
Class2：Ｐ（A1｜C2）、 Ｐ（A2｜C2）、 Ｐ（A3｜C2）

然後再把計算的結果相乘，在乘上P（C）的機率

Class1：Ｐ（A1｜C1）* Ｐ（A2｜C1）* Ｐ（A3｜C1）* Ｐ（C1）
Class2：Ｐ（A1｜C2）* Ｐ（A2｜C2）* Ｐ（A3｜C2）* Ｐ（C2）

最後取最大的機率來代表未知記錄的分類

舉例說明：

目標Class為Evade，其分類為Yes與No，因此P（Yes）＝ 3/10，P（No）＝7/10
而屬性的機率，則為P（A｜C）＝Ak / Nk，Nk為C分類下有多少數量，Ak為屬性A於C分類底下的數量，比方說P（Refund＝Yes｜Evade＝No）＝ ３/7

前面提到了，遇到連續行的屬性值（如上表中的Taxable Income），除了離散化（Discretize）與二元化（Two-Way Split）兩個方法外，這裡邊在介紹一個新的方法，利用機率密度估計（Probability density estimation）。

若要使用機率密度來估計的話，首先要假定屬性的值屬於常態分配。在用數據來算機率分布（如平均數與標準差），接著我們就可用來估計連續型態的 P（A｜C），其機率分布公式如下：

假設我們要求 P（Income＝120｜Evade＝No），其中假如Class＝No，其平均數為110，變異數為2975，標準差為54.54。

既然學會了機率的算法，接著我們套用一個未知屬性的資料X其 Refund＝No，Married，Income＝120K，求他的實際分配在哪個類別。
因為我們有兩個目標屬性Yes與No，故必須計算 P（X｜Class＝No）與 P（X｜Class＝Yes）
P（X｜Class＝No）
＝P(Refund=No｜Class＝No) * P(Married｜Class＝No) * P(Income＝120K｜Class＝No)
＝ 4/7 * 4/7 * 0.0072＝0.0024

P（X｜Class＝Yes）
＝P(Refund=Yes｜Class＝Yes) * P(Married｜Class＝Yes) * P(Income＝120K｜Class＝Yes)
＝ 1 * 0 * 1.2 * 10的-9次方 ＝0
因為 P（X｜Class＝No）＞P（X｜Class＝Yes）
所以 X屬於No

因此總結單純貝氏分類的特性：
1.對於雜訊能有想當好的處理能力（因為其機率分配很低）
2.對於遺漏值可以忽略不計
3.能夠處理屬性不相關的資料（因為假設屬性間互相獨立）
4.若屬性間有相關，會提高誤判的機率（就要改用其他方式如貝氏信念網路BBN）

４. 課後作業