授課教授:交通大學 交通運輸研究所 陳穆臻 教授
參考書籍:Introduction to Data Mining, Tan, P. T., Steinbach, M., Kumar,. Vipin
1. 群集分析(Cluster Analysis)
2. 群集的種類(Types of Cluster)
3. K-Means群集演算法(K-Means Algorithms)
4. 階層式群集分析 (Hierarchical Clustering )
5. 密度為基礎分群法(DBSCAN)
=========================
1. 群集分析(Cluster Analysis)
就是找出目標相關的資料,以及區分出沒有相關的資料
而哪些方式並不是群集分析呢?
監督式學習,因為本身已經擁有分類的屬性存在
簡單分割,像是單純的把學校學生用姓名筆劃依序排列好
結果查詢,像是搜尋引擎所得到的結果也不是群集分析
分群其實是相當模稜兩可的事情,要定義分群取決於資料的特性與使用者的育設立場
群集分析常見分成兩種方式
1. 劃分式的群集 (Partitional Clustering)
指採不重疊的方式劃分,將原有的資料分到不同的子集合中
將資料組織成一個樹狀結構,每次群集都會做一次相似度比對,將最近的資料納入
=========================
2. 群集的種類(Types of Cluster)
這一段將介紹群與群之間的樣式,可以有哪幾種變化
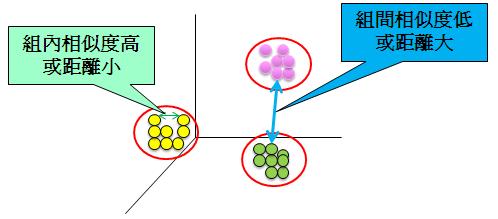
1. 分散良好的群集(Well-Separated)
即為,群組內的資料相似度都相當高,而群組間的相似度都相當低
2. 已中心點為基礎的群集(Center-Base)
即為群集內的資料點都相當接近群集的中心點,而較遠離其他群集的中心點
即使群與群之間相當接近,紅色群集中最遠點,依舊不會被分到綠色群集中
而中心點為基礎中有兩個相當重要的名詞如下:
(1) 群集的質心 Centroid
(2) 群集的最中心資料點 Medoid
3.連串的群集(Contiguity-Based)
這類的群集通常有一種圖形關係,群中資料點可能只會跟一個點相似,不是任何群中的點都有相似,用圖比較好解釋
圖中,有橘色與黃色兩個群集,很明顯可以看到,資料點1與資料點2是相似的點
但是,資料點1與資料點3來看的話,反而就相當遠,甚至會覺得資料點1應該是在橘色的群之中。
4.密度為基礎的群集(Density-Based)
透過單位面積內的資料密集度作為分割,密集度越高則被分在同一個群組內
5.概念群集(Conceptual Clusters)
這是一個相當複雜的群集狀況,群集的分佈可以看的出擁有共同的性質或像是一種概念分布,比方說下圖兩個圓環內的資料屬於同一群組,但在演算法上是很難做個表達
=========================
3. K-Means群集演算法(K-Means Algorithms)
這是一個相當基本的劃分群集演算方法,其中K的意思是要找出K組群集,Means則為群組質心,綜合來說就是尋找出K組群集,已群集質心作為相似度基準
K-Means的演算法相當的簡單,步驟如下:
1:先預設要找K組群集(可電腦選或人工植入)
2:repeat(進入迴圈)
3: 將資料點分群至K的群集中
4: 重新計算K個分群的各個質心
5:until(回到第二步)終止條件為當K個群集質心不再更動為止
演算法備註:
最一開始的K個群集的質心是隨機選取的。
利用歐式幾何位置來計算資料點與質心的距離。
K-Means演算法會在幾次迭代計算後收斂。
如果計算要太久的話,折衷方案是質心的變動很不大,則可結束計算。
K-Means的複雜度為:資料點的數量 * K個群集 * 迭代的次數 * 屬性的維度
下圖為K-Means的迭代計算過程,可以看到要一直不斷重新計算質心,重新分群
然而,問題來了!
K-Means的初始群集質心是隨機挑選的,所以可能會造成相當多不同的分群結果
為了要解決這樣的問題,常常會採取執行多次,找出一次較好的解,而何謂較好的解?
為了找出較好的解,我們必須對每次K-Means的結果做個評量
而K-Means的評量指標叫做平方誤差總和( Sum of Squared Error, SSE),公式如下:
其中,K為分群的數量、Ci為第i個分群集、Mi是分群質心、X為分群中的資料點
意思是,計算加總所有的分群裡頭每個資料點與質心距離的平方。
儘管有了評量指標,但K-Means仍然存在這不少問題,光是要找出一個最佳解,其機率就已經是小道不行,以及容易產生空集合(有的分群根本分不到東西)
解決的空集合辦法有下列幾種:
1.選擇較對SSE有幫助的質心
2.選擇擁有較高的SSE的質心
3.複合上述動作
解決初始質心的方法有下列幾種:
1.多跑幾次(但機率太低)
2.用樣本與層級分群來尋找初始質心
3.一次丟多個初始質心,然後找分布最廣的點
比方說我們要做 K=3的 K-Means,我們一開始就先設10個點,然後找分的最散的三個
4.前處理方法(做正規化與去除離群值)
5.事後處理(切割SSE太大的群,合併SSE太小的群,移除沒有什麼資料的群)
6.Bisecting K-Means群集演算法
其演算法步驟如下:
1. 初始時,將K設為1,即整個只有一個群
2. Repeat(進入迴圈)
3. 從清單中挑出一個群組來做處理
4. for i=1 to 預設的迴圈參數 do (做總共預設參數次的計算)
5. 採用基礎的K-Means演算法平分我們剛剛挑出來的群組
6. end for (完成for迴圈)
7. 把剛剛在迴圈中做出來的所有結果傭有最小SSE的兩個分群,加到我們的清單
8. Until 終止條件為直到清單分群的數量等於我們預設的K組分群
=========================
4. 階層式群集分析 (Hierarchical Clustering )
將資料點組織成一個有階層關係的樹枝狀架構,也輕易的利用圖形化來表達
階層式集分析的好處,不用預先設定要分成多少集群,利用砍樹的方式就可以分群了!
比方說上圖,我想要分成三群,一下就可以看出把距離設=3,則123為一群,45一群
而階層式群集分析,主要兩種描述方式集合式與切割式兩種,就是樹的成長方式由下往上與由上往下兩種方式生長
而基本的階層式群集演算法步驟如下:
1. 計算距離矩陣
(一開始是資料點間的距離,接著是資料點跟群集、最後是群集與群集)
2. 令每個資料點都是一個獨立的群集
3. Repeat(迴圈開始)
4. 結合兩個最相似的群集
5. 更新距離矩陣
6. Until 終止條件為匯聚成只剩下一個群集為止
從其中可以看到,最關鍵的步驟就是「怎麼計算群集間的距離」,不同的評估方式會產生不同的距離結果
而距離的計算方式,常用的有下面幾項
1. MIN or Single Link,指的是群集間最短距離
2. MAX or Complete Link ,指的是群集間最長的距離
3. Group Average ,指的是群集間的每個點之間的距離平均
4. Distance Between Centroids ,兩個集群的質心距離
5. 其他的方法,如:Ward's Method,採用均方誤差
=========================
5. 密度為基礎分群法(DBSCAN)
DBSCAN是 Density-Based Spatial Clustering of Applications with Noise 縮寫
這是一個已密度為基礎的分群方式,用密度的概念剃除不屬於所有分群資料的雜訊點
而DBSCAN的一些名詞定義如下:
1. Eps = Density = 以資料點為圓心所設的半徑長度
2. Core Point(核心點):以核心點為半徑所圍繞出來的範圍能包含超過我們指定的數量
3. Border Point( 邊界點):被某個核心點包含,但以他為中心卻沒辦法包含超過我們指定的數量。
4. Noise Point(雜訊點):不屬於核心點,也不屬於邊界點,即為雜訊點。
5. 密度相連:如果兩個核心點互為邊界點的話,則可把兩個核心點合併在同一個群組中
而DBSCAN的演算法步驟,如下:
1. 將所有的點做過一次搜尋,找出核心點、邊界點、雜訊點
2. 移除所有雜訊點
3. 設立一個「當前群集編號」的變數=0
4. for 1 到 最後一個核心點 do
5. 假設 這個核心點並沒有被貼上群組編號 則
6. 那就把「當前群集編號」的變數 + 1
7. 把「當前群集編號」給這個被抽出的核心點
8. 結束這個假設
9. for 這個核心點在密度相連後所有可以包含的點 do
10. 假設 這個點還沒有被貼上任何群組編號 則
11. 把這個點貼上「當前變數的編號」
12. 結束假設
13. 結束for迴圈
14. 結束for迴圈
也就是說一開始我們找到核心點1,但他還沒有被分到群組,所以我們給他群組1的編號
接著,把這個核心點1透過密度相連後所有包含的點,通通給群組1的編號
即可完成群組1的分類!